Resolución de problemas de seno y coseno de trigonométrica
Espero que esta información ayude para resolver muchas dudas
Triángulo rectángulo
Recordamos que un triángulo es rectángulo cuando tiene un ángulo recto, es decir, un ángulo de 90 gradosDe los tres lados del triángulo, se llama hipotenusa al lado opuesto al ángulo recto. Los otros dos lados se denominan catetos: también podemos medir el angulo desde el punto de partida o sea desde el inicio.
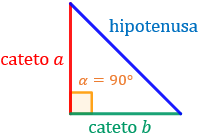
Sin embargo, en ocasiones no conocemos dos lados, pero sí conocemos uno de los otros dos ángulos no rectos. En estos casos es cuando utilizamos el seno y el coseno.
Seno y coseno
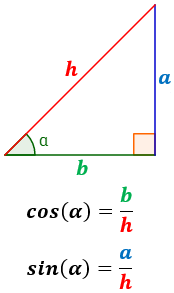
De forma análoga, el seno de se define como el cociente del lado opuesto al ángulo y la hipotenusa.
Nota: si cambiamos de ángulo, cambian los numeradores:
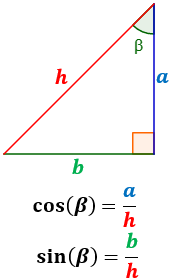
Nosotros utilizaremos y .
Regla mnemotécnica: el COseno es el lado COntiguo entre la hipotenusa y el senO es el lado Opuesto entre la hipotenusa.
Tangente
La tangente del ángulo es el cociente del seno y del coseno de dicho ángulo: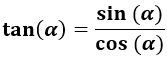
La tangente del ángulo puede escribirse como y como , entre otras.
No utilizaremos la tangente en esta página.
Arcoseno y Arcocoseno
Si conocemos el seno (o coseno) de un ángulo , podemos conocer el ángulo mediante la función arcoseno (o arcocoseno).En esta página sólo utilizaremos estas funciones en la calculadora con las teclas (arcoseno) y (arcocoseno).
Nota: hay que tener cuidado con las funciones arcoseno y arcocoseno ya que hay ángulos que tienen el mismo seno o coseno. Por ejemplo, el seno de 45º es el mismo que el de 135º:
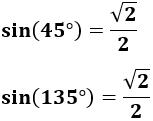
Nota previa: para simplificar los cálculos, aproximaremos las razones trigonométricas con dos o tres decimales por redondeo o por truncamiento. Como consecuencia, los resultados pueden ser no exactos.
 Calcular el precio del cable si cada metro cuesta 12$.
Calcular el precio del cable si cada metro cuesta 12$.
Problema 1
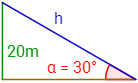
Se desea sujetar un poste de 20 metros de altura con un cable que parte de la parte superior del mismo hasta el suelo de modo que forme un ángulo de 30º.
Solución
Como conocemos el lado opuesto, , utilizamos el seno para calcular la hipotenusa del triángulo:
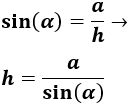 Sustituimos el ángulo y el lado:
Sustituimos el ángulo y el lado:
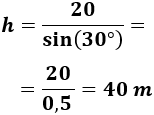 Luego el cable debe medir 40 metros y su precio es de 480$:
Luego el cable debe medir 40 metros y su precio es de 480$:
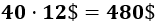
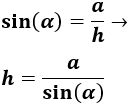
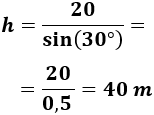
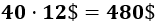
Problema 2
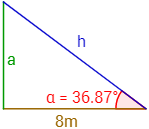
Solución
Como la altura
es el cateto opuesto al ángulo, utilizaremos el seno:
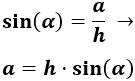
Pero como necesitamos calcular la hipotenusa del triángulo, utilizamos el coseno:
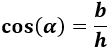
Sustituimos los datos:
La hipotenusa mide
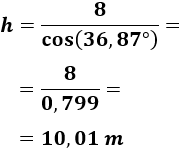
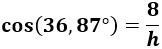
Por tanto, la altura del árbol es
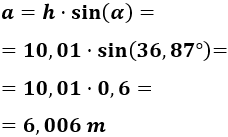
Problema 3
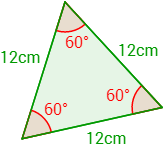
Ayuda: la mediana es la distancia del segmento que une un vértice con el punto medio del lado opuesto a éste.
Solución
La mediana forma un triángulo rectángulo:
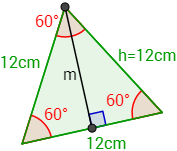
Del triángulo conocemos tres ángulos: uno mide 60º, otro 30º y el otro 90º. También conocemos su hipotenusa .
Utilizamos el seno para calcular la mediana :
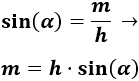
Sustituimos los datos:
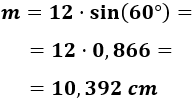
Luego la mediana mide 10,392 centímetros
Problema 4
Escribir una fórmula para calcular la longitud de la mediana de un triángulo equilátero de lado .Ayuda: la fórmula se puede obtener rápidamente a partir del problema anterior.
Solución
Como los lados del triángulo miden en lugar de 12cm, sólo tenemos que cambiar 12 por en el problema anterior ya que los ángulos son iguales.
La fórmula es

O bien, si aproximamos el seno,

Problema 5
Del siguiente triángulo rectángulo se conocen sus dos catetos: uno mide 4m y el otro mide 3m: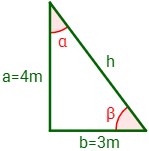
Solución
Como el triángulo es rectángulo, aplicamos el teorema de Pitágoras para calcular la hipotenusa:
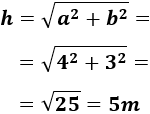 La hipotenusa mide 5 metros.
La hipotenusa mide 5 metros.
Para calcular los ángulos podemos utilizar, por ejemplo, el seno:
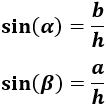 Como conocemos los catetos y la hipotenusa, podemos calcular el seno de los ángulos:
Como conocemos los catetos y la hipotenusa, podemos calcular el seno de los ángulos:
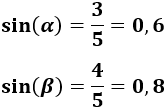 Finalmente, para calcular los ángulos sólo debemos utilizar la función arcoseno:
Finalmente, para calcular los ángulos sólo debemos utilizar la función arcoseno:

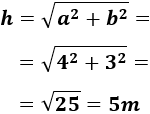
Para calcular los ángulos podemos utilizar, por ejemplo, el seno:
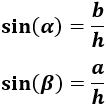
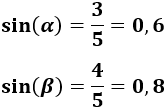

Problema 6
Calcular el radio de la circunferencia que se obtiene al utilizar un compás cuyos brazos miden 10cm si éstos forman un ángulo de 50º.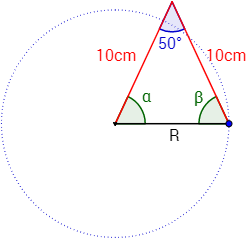
Solución
El compás junto con el radio forma un triángulo isósceles. Lo que significa que los ángulos y son iguales.
Como la suma de los ángulos (interiores) de un triángulo es siempre 180º, podemos calcular :
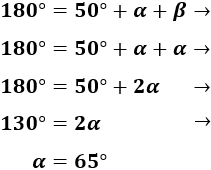
Al representar la altura , tenemos un triángulo rectángulo:
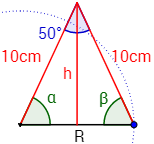
Si llamamos a la mitad del radio y aplicamos el coseno, tenemos
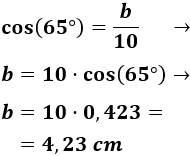
Por tanto, el radio de la circunferencia mide 8,46cm:
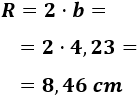
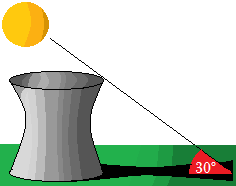
Problema 7
Solución
Llamamos a la altura y a la hipotenusa. Por el seno:
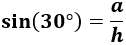 Despejamos la altura:
Despejamos la altura:
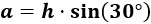 Necesitamos calcular la hipotenusa. Por el coseno tenemos
Necesitamos calcular la hipotenusa. Por el coseno tenemos
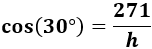 Despejamos la hipotenusa:
Despejamos la hipotenusa:
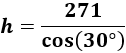 Sustituimos la hipotenusa:
Sustituimos la hipotenusa:
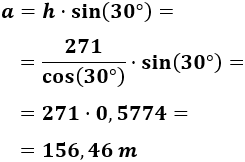 Por tanto, la altura de la torre es de unos 156,46 metros.
Por tanto, la altura de la torre es de unos 156,46 metros.
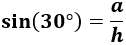
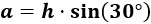
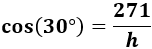
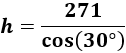
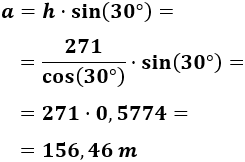
Problema 8
Las ciudades A, B y C son los vértices de un triángulo rectángulo: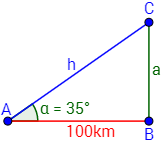
Solución
Por el seno y por el coseno tenemos las siguientes relaciones:
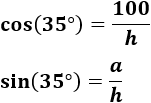
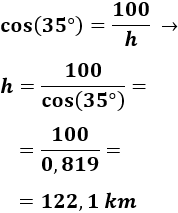
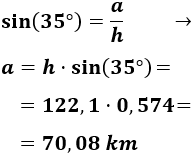
Problema 9
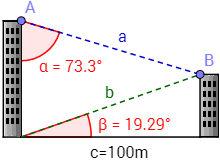
¿Puede Miguel calcular la altura de los edificios con los tres datos con los que cuenta? En caso afirmativo, ¿cuál es la altura de cada uno?
Solución
Sí es posible calcular la altura de ambos edificios.
El ángulo forma parte de un triángulo rectángulo. Representamos el segmento para formar un triángulo rectángulo con el ángulo :
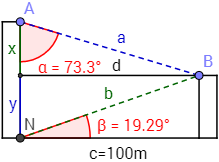 Obsérvese que el segmento mide 100 metros, que la altura del edificio más alto es la suma de los catetos e y la altura del otro edificio es .
Obsérvese que el segmento mide 100 metros, que la altura del edificio más alto es la suma de los catetos e y la altura del otro edificio es .
Por el seno y el coseno, tenemos las siguientes relaciones para el ángulo :
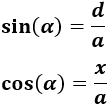 Como conocemos y , podemos calcular .
Como conocemos y , podemos calcular .
Primero, calculamos :
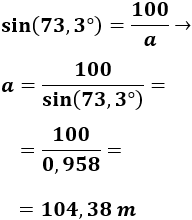 Ahora, calculamos :
Ahora, calculamos :
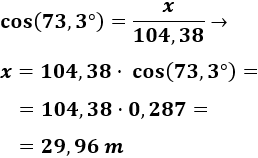 Por el seno y el coseno, tenemos las siguientes relaciones para el ángulo :
Por el seno y el coseno, tenemos las siguientes relaciones para el ángulo :
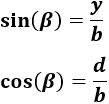 Como conocemos y , podemos calcular .
Como conocemos y , podemos calcular .
Primero, calculamos :
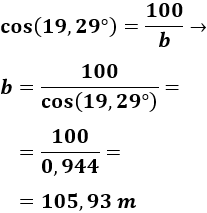 Ahora, calculamos :
Ahora, calculamos :
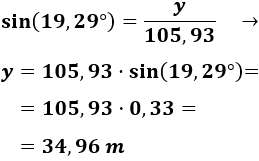 Por tanto, la altura del edificio alto es
Por tanto, la altura del edificio alto es
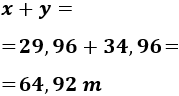 Y la altura del otro edificio es 34,96 metros.
Y la altura del otro edificio es 34,96 metros.
El ángulo forma parte de un triángulo rectángulo. Representamos el segmento para formar un triángulo rectángulo con el ángulo :

Por el seno y el coseno, tenemos las siguientes relaciones para el ángulo :
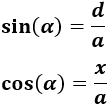
Primero, calculamos :
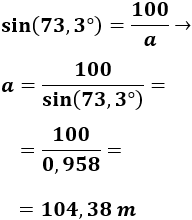
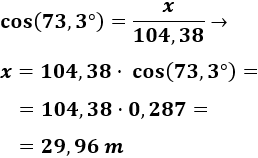
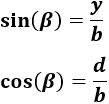
Primero, calculamos :
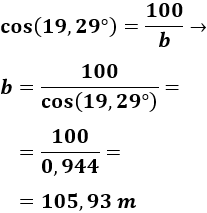
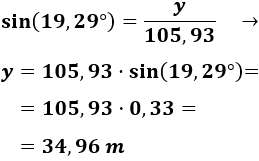
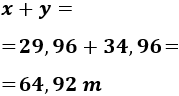
Problema 10 (dificultad alta)
Desde una determinada distancia, una bandera situada en la parte superior de un torreón se observa con un ángulo de 47º. Si nos acercamos 17,8 metros al torreón, la bandera se observa con un ángulo de 75º.
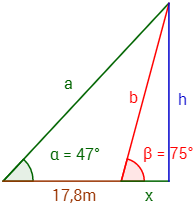
Calcular la altura a la que se encuentra la bandera.
Nota: para simplificar los cálculos podemos escribir (tangente de ) en lugar de .
Las relaciones que tenemos son
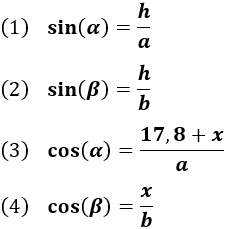
Escribimos la tangente de :
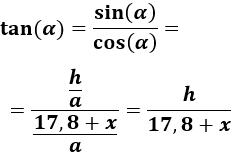
De donde podemos despejar :
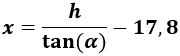
Escribimos la tangente de :
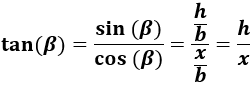
De donde despejamos la altura :
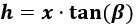
En la ecuación obtenida, sustituimos por la expresión obtenida anteriormente:
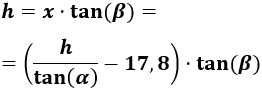
Resolvemos la ecuación:
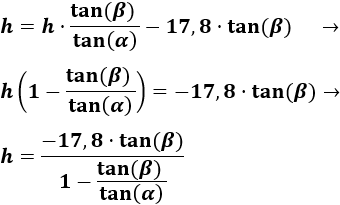
Sustituimos los datos:
Las relaciones que tenemos son
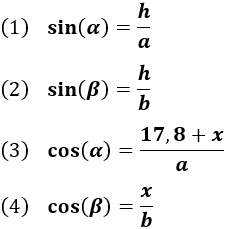
Escribimos la tangente de :
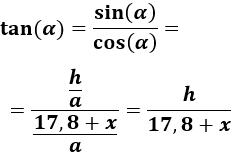
De donde podemos despejar :
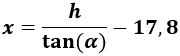
Escribimos la tangente de :
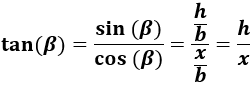
De donde despejamos la altura :
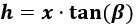
En la ecuación obtenida, sustituimos por la expresión obtenida anteriormente:
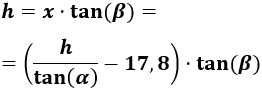
Resolvemos la ecuación:
sustituimos datos

Por tanto, la bandera se encuentra a unos 26,78 metros de altura.
Te invito a que veas el siguiente vídeo para mejor explicación.
Este trabajo fue una referencia de el siguiente link
es un tema que esta muy vien explicado
ResponderBorrarBuen tema interesante
ResponderBorrargran tema para poner en practica
ResponderBorrarque interesante, gracias por tu información
ResponderBorrarEl tema me ha servido muchisimo
ResponderBorrarbuen tema muy esplicado
ResponderBorrar